Peirce's law

In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely implication.

In propositional calculus, Peirce's law says that ((P→Q)→P)→P. Written out, this means that P must be true if there is a proposition Q such that the truth of P follows from the truth of "if P then Q". In particular, when Q is taken to be a false formula, the law says that if P must be true whenever it implies the false, then P is true. In this way Peirce's law implies the law of excluded middle.

Peirce's law does not hold in intuitionistic logic or intermediate logics and cannot be deduced from the deduction theorem alone.

Under the Curry–Howard isomorphism, Peirce's law is the type of continuation operators, e.g. call/cc in Scheme.[1]

Contents

History

Here is Peirce's own statement of the law:

A fifth icon is required for the principle of excluded middle and other propositions connected with it. One of the simplest formulae of this kind is:
{(x → y) → x} → x.
This is hardly axiomatical. That it is true appears as follows. It can only be false by the final consequent x being false while its antecedent (x → y) → x is true. If this is true, either its consequent, x, is true, when the whole formula would be true, or its antecedent x → y is false. But in the last case the antecedent of x → y, that is x, must be true. (Peirce, the Collected Papers 3.384).

Peirce goes on to point out an immediate application of the law:

From the formula just given, we at once get:
{(x → y) → a} → x,
where the a is used in such a sense that (x → y) → a means that from (x → y) every proposition follows. With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of x follows the truth of x. (Peirce, the Collected Papers 3.384).

Warning: ((x→y)→a)→x is not a tautology. However, [a→x]→[((x→y)→a)→x] is a tautology.

Other proofs of Peirce's law

Showing Peirce's Law applies does not mean that P→Q or Q is true, we have that P is true but only (P→Q)→P, not P→(P→Q) (see affirming the consequent).

simple proof: 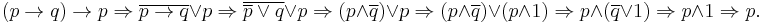(p \rightarrow q) \rightarrow p \Rightarrow \overline{p \rightarrow q} \or p \Rightarrow \overline{\overline p \or q} \or p \Rightarrow (p \and \overline q) \or p \Rightarrow (p \and \overline q) \or (p \and 1) \Rightarrow p \and (\overline q \or 1) \Rightarrow p \and 1 \Rightarrow p.

Using Peirce's law with the deduction theorem

Peirce's law allows one to enhance the technique of using the deduction theorem to prove theorems. Suppose one is given a set of premises Γ and one wants to deduce a proposition Z from them. With Peirce's law, one can add (at no cost) additional premises of the form Z→P to Γ. For example, suppose we are given P→Z and (P→Q)→Z and we wish to deduce Z so that we can use the deduction theorem to conclude that (P→Z)→(((P→Q)→Z)→Z) is a theorem. Then we can add another premise Z→Q. From that and P→Z, we get P→Q. Then we apply modus ponens with (P→Q)→Z as the major premise to get Z. Applying the deduction theorem, we get that (Z→Q)→Z follows from the original premises. Then we use Peirce's law in the form ((Z→Q)→Z)→Z and modus ponens to derive Z from the original premises. Then we can finish off proving the theorem as we originally intended.

Completeness of the implicational propositional calculus

Main article: implicational propositional calculus

One reason that Peirce's law is important is that it can substitute for the law of excluded middle in the logic which only uses implication. The sentences which can be deduced from the axiom schemas:

(where P,Q,R contain only "→" as a connective) are all the tautologies which use only "→" as a connective.

Notes

  1. ^ A Formulae-as-Types Notion of Control - Griffin defines K on page 3 as an equivalent to Scheme's call/cc and then discusses its type being the equivalent of Peirce's law at the end of section 5 on page 9.

References

Main article: Charles Sanders Peirce bibliography